『通常学級で役立つ算数障害の理解と指導法』は、学習障害の中の算数障害について、その指導ノウハウを通常学級の指導に取り入れる方法などを紹介している本。
学習障害児がつまずきやすい算数概念や学習は健常児もつまずきやすく、学習障害児にわかりやすい指導は健常児にとってもわかりやすい。
すなわち本書は、算数につまずきのあるすべての子どもにとって参考になると言えます。

通常学級で役立つ 算数障害の理解と指導法 みんなをつまずかせない! すぐに使える! アイディア48
算数障害の4つの領域
学習障害の「聞く」「話す」「読む」「書く」「計算する」「推論する」という領域の中で、算数障害は「計算する」「推論する」に困難がある場合を言います。
また算数障害は①数処理➁数概念③計算④数的推論(文章題)の4つの領域に整理できます。
算数障害の4つの領域
①数処理・・・数詞・数字・具体物の対応関係
➁数概念・・・序数性と基数性
③計算・・・数と数との操作(暗算、筆算)
④文章題・・・さまざまな数の変化や操作を推論する
「数えまちがい」「数字の読みまちがい・書きまちがい」・・・数処理が苦手な子
「数処理」とは、数の3つの側面、数詞・数字・具体物を対応させること。
「数処理」は計算の前段階であり、算数・数学では、まず数詞・数字・具体物の対応関係が習得されます。
・数詞:「いち、に、さん・・・」音としての数(聴覚的・言語的シンボル)
・数字:「1、2、3・・・」文字としての数(視覚的・言語的シンボル)
・具体物:「●●●・・・」数えられるものとしての数(視覚的で操作可能なもの)
数詞「いち、に、さん・・・」は音としての数(聴覚的・言語的)、数字「1、2、3・・・」は文字としての数(視覚的・言語的)、具体物は数えられるものとしての数(視覚的で操作可能なもの)というように、それぞれに関連する能力に特徴があります。
そのため、それぞれの能力が十分に伴っていない場合、例えば「数字は書けるが読めない」などのようなことが起こってしまいます。
数処理が苦手な子の例
数処理(数の変換)が苦手な子の例
☑・5と言いながら3本の指を出している。
☑・ものをよく数え間違えている。
☑・「ひゃくいち」を1001と書く。
☑・4501を読めない。「よん・ごじゅう・いち」などと読む。
数処理(数の変換)を失敗する原因
・正しい数唱ができていない
数を正しく数えるには、数を正しい順序で唱えること(=正しい数唱)が必要。
聴覚的な記憶力や継次処理能力(一つ一つの情報を時間的な順序で処理していく能力)に困難がある場合、数詞の系列(数の順番)を正確に覚えられないため正しい数唱ができない、すなわち、正しく数えられなくなってしまいます。
・数詞とモノの一対一対応ができていない
数を正しい順番で唱えられていても、1つのモノに1つの数詞を結びつけること(数詞とモノの一対一対応)ができていないと、正しく数を数えることができません。
目と手の協応(目で見た情報に合わせて体を動かす)や視覚的な短期記憶力(見たものをすぐに覚える力)が弱いと、モノを数えるとき、既に数えたものを覚えていられないために同じものを何度も数えてしまったり、逆に飛ばしてしまったりします。
・十進法位取りによる記数法が理解できていない
十進法とは、10のまとまりごとに1つ上の位に上げていく数の表し方のこと。
また数字を書く位置によって数の大きさを表すきまりのことを「位取り」と言い、十進法と位取りの原理によって,0から9の10個の数字を使って数を表す方法を「十進位取り記数法」といいます。
この「十進位取り記数法」が理解できていないと「さんじゅういち」を「301」と書いてしまったり、桁の大きい数字を読めなかったりと、大きな数の処理につまずいてしまうことがあります。
数処理が苦手な子への指導例
数詞・数字・具体物の対応がなかなか成立しない場合には、「すごろく」による指導が有効。
すごろく遊びでは、サイコロの目(ドットや数字)を声に出して数唱しながら1つ1つコマを動かしていくことで、数詞と数字(サイコロの目の数)と具体物(すごろくのマス)とを結びつけやすくなります。
サイコロの目(1・2・3)・・・数字
目の数だけ数える・・・数詞
すごろくのマス、サイコロの目(●や☆)・・・具体物
なお、すごろく遊びを行う際には、その子が理解できる数の範囲のサイコロを用いて行いましょう。
1しか理解できない場合のサイコロの目
☆、●、1、☆☆、●●、2
2までしか理解できない場合のサイコロの目
●、1、●●、2、●●●、3
3しか理解できない場合のサイコロの目
☆☆☆、●●●、3、☆☆☆☆、●●●●、4
「正確な数がわからない」・・・・序数性が理解できない子
数には序数性(順番をあらわす)と基数性(量を表す)という2つの側面があります。
序数性が理解できない子の例
「数の概念」のうち、順序としての数(序数性)が理解できていないと、おおまかな量はわかっても数を正確に操作することができません。
たとえば20個のキャンディーを3人で分けるとき、7個・6個・7個に分けて、個数の差に気がつかないということが起こります。
序数性が理解できない子の例
☑・1桁の数の順序はわかるが2桁以上の数の読み方が苦手
☑・41と14の違いがわからなくなってしまう
☑・数をおおまかに分けることはできるが、正確に計算することができない
序数性が理解できず正確な数がわからない原因
・数を順序よく唱えられない
序数性とは数の2つの側面のうちの1つで、数が系列であって、順序を表していること。
量としての数(基数性)はよく理解できているが順序としての数(序数性)が理解できない子は、同時処理能力にくらべて継次処理能力が低いため、数の系列がなかなか習得できない、つまり「いち、に、さん、し、ご・・・」と数を順序よく唱えられません。
そのため、ざっくりとしたおおよその数の量感はわかりますが、正確な数の理解が困難となってしまいます。
同時処理能力
・「全体から部分へ」という方向を踏まえる。
・物事の全体像をイメージし、情報と情報の関係を把握していく(全体→部分へ)
・視覚からの情報収集・理解が得意
継次処理能力
・情報を一つ一つ順番に理解し、それらをつないで全体を捉える(部分→全体へ)
・学習するときには始めから順序だてて行うことを好む。
・聴覚からの情報収集・理解が得意
・数字の配置による意味の違いがわからない
例えば41の「1」と14の「1」では、数字の配置により意味(あらわしている数)が違いますが、数字の配置の順番がわからないと、配置による意味の違いもわかりません。
そのため2桁以上の数字の読みがわからなかったり、書く時も41と14を混同してしまったりします。
序数性が理解できず正確な数がわからない子への指導例
序数性が理解できない場合には、数処理の指導でも使用した「すごろく」が有効。
ただし、すごろくを実施することが目的ではなく、その準備段階が指導のポイントとなります。
すごろくの台紙のマス(〇印)に、数詞を言いながら数字を書かせることで、数の順序をインプットしていきます。
数字の並びを組織的に見せるように、10ずつマスを書いていき、十進法規則性と数詞と数字を理解させていきます。
「およその量がわからない」・・・基数性が理解できない子
基数性の理解に問題がある場合は、数の「量」としての側面が理解できません。
基数性が理解できない子の例
☑・計算問題はできるが、数のまとまりを見つけたり分けたりることは難しい
☑・集合が理解きない
☑・数直線の問題が苦手
☑・線分図のどの辺りに指示された数がくるのかがわからない
☑・およその数の見当を立てるのが難しい
基数性が理解できず、およその量がわからない原因
基数性(数が「量」をあらわしていること)が理解できないと、数の操作はできても、数が示す意味や、数を操作することの意味がわかりません。
例えば、あそこの木のところまで何歩で行けるかをおおよそ予測することができなかったり、10個という数のまとまりを見つけることができないなど、集合という概念が理解できないことがあります。
それなのに、計算問題は計算の方法が分かって答えられることもあります。
このようなタイプの子の場合、計算問題はできても文章問題から立式することができず、小学校低学年のうちは問題が生じなくても、高学年になるに従い問題が出てくることがあります。
基数性が理解できず、およその量がわからない子の指導例
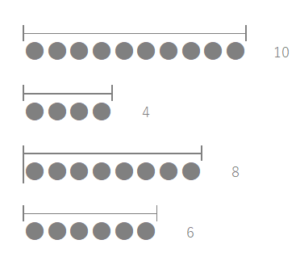
線分をわかりやすい分離量におきかえる
計算の操作ができても、5と14のどちらが多いかを具体的な量のイメージをもって言い当てられない場合、連続量を分離量に置き換える操作が有効。
最後に
①数処理・・・数詞・数字・具体物の対応関係
➁数概念・・・序数性と基数性
についてお伝えしました。
③計算・・・数と数との操作(暗算、筆算)
④文章題・・・さまざまな数の変化や操作を推論する
『通常学級で役立つ算数障害の理解と指導法』は、学習障害の中の算数障害について、その指導ノウハウを通常学級の指導に取り入れる方法などを紹介している本。 学習障害児がつまずきやすい算数概念や学習は健常児もつまずきやすく、学習障害児にわかり[…]

