2年生の算数の最重要ポイントといえば、『九九』。
この先の計算学習すべてに九九が絡んできますので、2年生で完全にマスターしておく必要があります。
しかしながら、九九をひたすら丸暗記させればOK、という訳ではありません。
九九が言えるようになる前に、かけ算の意味をしっかり理解しているかどうかが重要です。
そこでこちらの記事では、かけ算の意味を感覚的に理解できるオススメ教材『強育パズル かけ算・わり算が得意になる九九トレ』をご紹介します。

【宮本算数教室の教材】強育パズル かけ算・わり算が得意になる九九トレ 初級編 【小学校全学年用 算数】 (考える力を育てる)
「かけ算の意味」を正しく理解できていますか?
たとえば「2×5」というかけ算は、「2が5つ分」という意味。
これを「2+2+2+2+2」、すなわち「2を5回足したもの」と理解して、お子さんにもそのように説明している方もいらっしゃるかもしれませんが、少し意味が違います。
2×5とは、「1つにつき2つあるものが5つ分」ということ。
すなわち『1当たり量×いくつ分』で全体量を考えるというのが、かけ算の意味になります。
ちなみに「1当たり量」とは、1つのものに同じ数だけあるもの。
例えば
「ウサギの耳は1匹につき2つ」
「車のタイヤは1台につき4つ」
など、もともと数が決まっているものもあれば、
「おはじきを1人に2こずつ配る」
などの場合もあります。
「ウサギが5匹います。耳は全部でいくつあるでしょう?」の場合、
2(1匹あたりの耳の数)×5(ウサギの数)=10(全部の耳の数)
また、
「3個入りのケーキの箱が4個あります。ケーキはぜんぶでいくつでしょう?」の場合は、
3(1箱あたりのケーキの数)×4(箱の数)=12(全部のケーキの数)
となります。
この時、4×3でも答えは同じ12ですが、「3×4(3の4つ分)」と「4×3(4の3つ分)」では意味が違うので注意が必要です。
また、上記のように2×5を2+2+2+2+2(2を5回足したもの)のように足し算で考えていると、「2✕0=2」といった間違いをしてしまいがちです。
しかしながら、『1当たり量×いくつ分=全体量』というかけ算の意味を理解していれば、
2(1匹あたりの耳の数)×0(ウサギの数)=0(全体の耳の数)
すなわち、ウサギが1匹もいなければ耳の数は0になる、とわかります。
逆に、かけられる数が0の場合を、上記のケーキの箱の例で考えてみると、
0(1箱当たりのケーキの数)×5(箱の数)=0(全体のケーキの数)
つまり、空っぽの箱が何個あってもケーキの数は0。すなわち0×5=0である、ということがわかります。
『強育パズル かけ算・わり算が得意になる九九トレ』の内容
私の教室の小学生クラスで使用している『強育パズル かけ算・わり算が得意になる九九トレ』は、かけ算の意味を理解しながら定着させるのにおすすめの教材。

強育パズル かけ算・わり算が得意になる九九トレ 初級編 【小学校全学年用 算数】 (考える力を育てる)

強育パズル かけ算・わり算が得意になる九九トレ 中級編 【小学校全学年用 算数】 (考える力を育てる)

強育パズル かけ算・わり算が得意になる九九トレ 上級編 【小学校全学年用 算数】 (考える力を育てる)
なお実際に使用しているのは、こちらの教材の旧バージョンになります。

この『強育パズル かけ算・わり算が得意になる九九トレ』の著者は、宮本算数教室を主催する宮本哲也さん。
別の記事でご紹介させていただいた『賢くなるパズル』や『算数と国語を同時に伸ばすパズル』と同じです。
「ににんがし、にさんがろく・・・・・・」、これを言葉だけで丸暗記しても意味がありません。
九官鳥に言葉を覚えさせるのと同じです。
と書かれているように、九九をただ呪文のように丸暗記するのではなく、しっかりとかけ算九九の意味を理解しながら定着させることができる教材です。
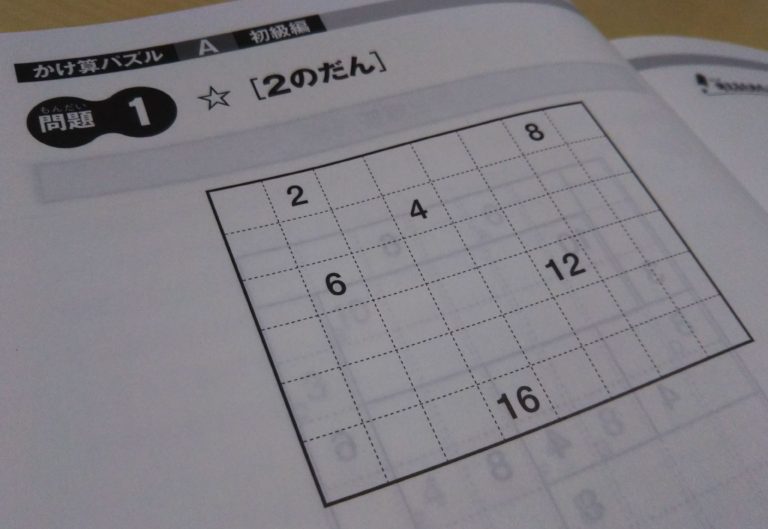
問題のパターンはすべて同じ。

①図のマスを1つもあまらないように正方形または長方形に分けます。
②1つの正方形または長方形の中には必ず数字が1つ入ります。
③②の数字はその正方形または長方形に含まれるマスの数を表します。
④同じマスを2つの正方形または長方形が同時に使うことはできません。

初級編では、各問題に「2のだん」などの指示があるので、縦か横のいずれかのマスの数が決まります。
(2の段で数字が10なら、縦2×横5マスか、縦5×横2マスのどちらかになります。)

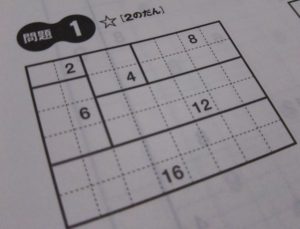
このようにして分けられたマス目を見れば、「ににんがし、にさんがろく、にしがはち、にごじゅう・・・」と呪文のように唱えていた九九の意味が目で見て理解できる、という訳です。
中級以降は「2のだん」などの指示がなく、数字が12なら「1×12」か「2×6」か「3×4」と考える、すなわち『約数』を考えることになります。


このように、『強育パズル かけ算・わり算が得意になる九九トレ』はかけ算やわり算を、単に暗記や数字上の操作だけでなく、視覚でとらえ感覚的に理解するのに役立ちます。
ちなみに教室では、まだかけ算を習っていない段階から取り組んでいます。
はじめはマスの数を1つずつ数えながら取り組むことができますし、後にかけ算を習った時に「そういうことか!」とつながり理解が深まります。
最後に
「九九はひたすら丸暗記!」と思っていらっしゃる方も多いと思いますが、まずは理解をともなってこそ。
”かけ算の意味”について親御さんもしっかり理解をした上で、お子さんにも、本質を理解しながら定着できるような取組をさせてあげてくださいね!
なおこちらの記事では、『強育パズル かけ算・わり算が得意になる九九トレ』の他にも算数的思考力をやしなう小学校低学年向けおすすめのドリル・問題集をご紹介していますので、参考にしてみてくださいね!
*関連記事:小学校低学年の算数:思考力系おすすめドリル・問題集まとめ
算数のドリル・問題集というと、いわゆる計算ドリルのようなものをイメージされる方も多いかと思いますが・・・ ひとくちに算数の力と言っても、その中身はさまざま。 算数で求められる力のうち、何を伸ばしたいかによっても取り組む内容は違ってき[…]